Diffractive Optics

VIAVI designs and fabricates diffractive elements with both binary and analog phase profiles.

Binary elements attain efficiencies near 80% (neglecting surface losses) and often represent cost-effective solutions if feature sizes are too small for analog fabrication and if the desired pattern has centrosymmetry. Centrosymmetry means that if I(m,n) represents the intensity at diffraction order (m,n) then I(-m,-n) = I(m,n). If the pattern or spot array to be produced has centrosymmetry then it can be manufactured with a binary phase mask, otherwise it needs to be continuous.

VIAVI also produces analog, continuous-phase diffractive elements.

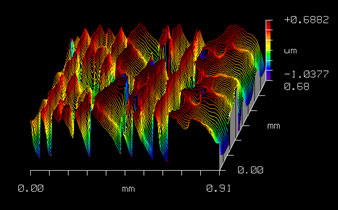
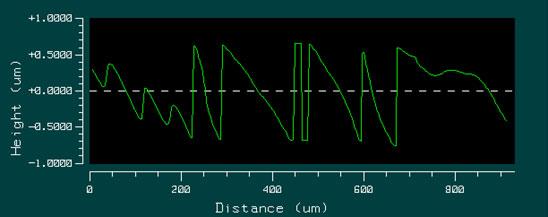
Continuous elements reach efficiencies over 90% (neglecting surface losses) and enable the production of more general patterns.

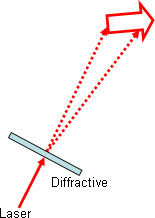
Diffractive elements typically operate under collimated, coherent illumination in the geometry shown below, with an optional focusing lens.

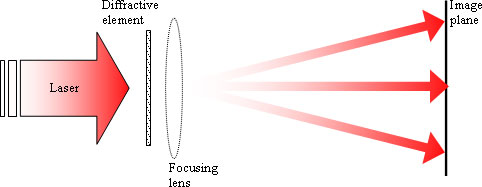
The typical problem is to calculate the diffractive element surface structure, given the desired intensity distribution in the image plane.

VIAVI has developed rigorous design and modeling codes that optimize the diffractive element maximizing performance for the specific manufacturing method.

Here are some of the diffractive elements VIAVI designs and manufactures:

• Diffractive lenses
• Beam splitters (spot arrays)
• Diffractive diffusers
• Corrector plates

Diffractive lenses

Diffractive lenses can be used to reduce the number of elements in conventional lens systems and eliminate the need for exotic materials in correcting chromatic aberrations.

Diffractive lenses are very thin elements with total depth height equal to λ/(n – 1), where λ is the operating wavelength and n is the index of refraction. A diffractive lens is composed of a series of zones that become finer towards the edge of the lens.

As a general rule, diffractive elements work best at a single wavelength. At any other wavelength the efficiency as well as image contrast are reduced.

However, for applications where one has a certain number, 2, 3, …, of discrete wavelengths it is possible to design a diffractive lens that shows 100% theoretical efficiency at each of those wavelengths. We call this particular design a “MOD” lens, which stands for “multi-order diffractive” lens.

The MOD lens* is a little deeper than the conventional diffractive lens by an integer factor p. At the same time the zone size increases.

*Useful references on MOD lenses:

1. D. Faklis and G. M. Morris, “Spectral properties of multi-order diffractive lenses,” Appl. Opt. 34, 2462 (1995).
2. D. Faklis and G. M. Morris, US Patent #5,589,982

Beam splitters (spot arrays)

A common use of a diffractive element is the splitting of a laser beam into an array of spots. In this case, a generally collimated beam incident on the element is separated into an array, either 1D or 2D.

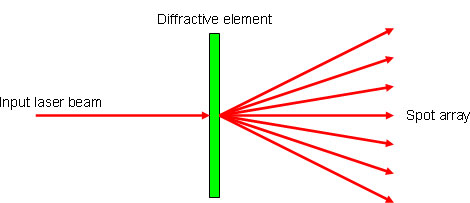
The diffractive element that produces a beam splitter is basically a grating with some complicated shape that generates the desired distribution of spots. There are two basic design approaches to producing a diffractive beam splitter: binary and analog solutions. The binary solution is one of the most common and useful approaches to produce a beam splitter if the desired spot distribution is centrosymmetric.

Here is an example of a 25×5 spot array illustrating some of the main features of binary designs.

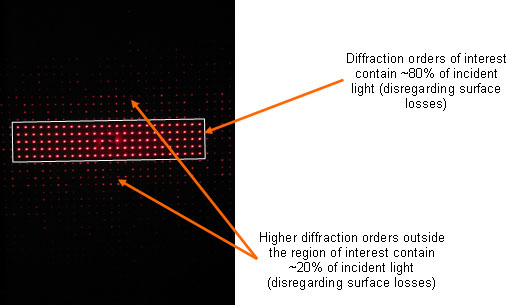
Analog design solutions can reach theoretical efficiency above 90% but require more sophisticated production techniques. VIAVI has developed both design and analysis models to generate and evaluate solutions for diffractive elements in general and beam splitters in particular. We can also produce these elements in either binary or analog format. To produce analog diffractives we utilize our laserwriting technique to produce a continuously varying surface that produces the desired spot distribution.

The example below shows a portion of the surface pattern that projects an arrow.

Diffractive diffusers

Diffractive elements can also be used as diffusers to provide controlled illumination for certain specialized applications such as lithographic illumination systems. The main advantage of diffractive diffusers compared to refractive ones, such as our Engineered Diffusers™, is the sharp intensity fall-off, which is as wide as the diffraction-limited spot corresponding to the incident beam size at the operating wavelength. Diffractive diffusers can be implemented with binary or analog phase functions with efficiencies of about 80% and 90-95%, respectively.Diffractive circular diffuser implemented with a binary phase function.

This example illustrates a common issue with diffractive diffusers: zero order. This diffuser is being illuminated with a HeNe laser, but its phase depth is not exactly correct for this source. As a result, the zero order is brighter than the other orders. Other Examples of light distributions generated by diffractive diffusers with binary phase function. Analog phase functions can also be used for higher efficiency and lower sensitivity to depth errors that minimizes zero order, if the scatter angles are small.

Corrector plates

In some applications a particular wavefront is required at some point of the optical system but, for whatever reason, the actual wavefront does not show the desired form.

If the wavefront deviation from the ideal is consistent and repeatable, a corrector plate can be introduced to correct the wavefront by inducing the appropriate phase delay at various points of the aperture to produce the desired wavefront.

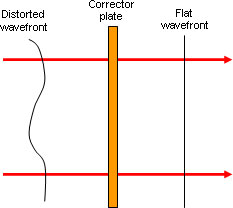In a typical wavefront corrector application the input wavefront contains some distortion that needs to be eliminated to produce a uniform, flat wavefront. The corrector plate introduces phase delay that matches the input wavefront to eliminate the undesirable variations. Corrector plates need to be aligned with the incident wavefront and work best if the distortion in the wave front is repeatable and stationary.

VIAVI laserwriting technology enables the production of corrector plates with high accuracy even if it requires correction of high-frequency wavefront distortion.